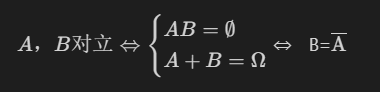事件与概率

随机试验

E为一个试验，当E满足：

  • 相同条件下可重复
  • 试验的结果具有多样性；试验前所有可能结果已知
  • 试验前不确定何种结果发生

满足以上三个条件的试验称为随机试验

如：

  • 投币[正面，反面]
  • 投骰子[1，2，3，4，5，6]

样本空间

E为随机试验，E的所有可能的基本结果而成的集合，称为E的样本空间，记为 Ω

如：扔骰子E

  • Ω = [1，2，3，4，5，6]
  • A = [2，4，6]

A是一个事件，但不是一个基本事件

随机事件

E为随机试验，Ω为E的样本空间，Ω的子集称为随机事件，简称事件

  • ∅⊂Ω

    • ∅–不可能事件

  • Ω⊂Ω

    • Ω–必然事件

事件的关系运算

运算

设A，B为事件

  • 和

    • A或者B发生的事件称为A，B的和事件，记A+B

  • 积

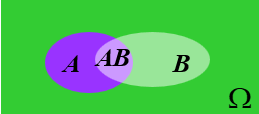
    • A和B同时发生的事件称为A，B的积事件，记为AB（或者A∩B）

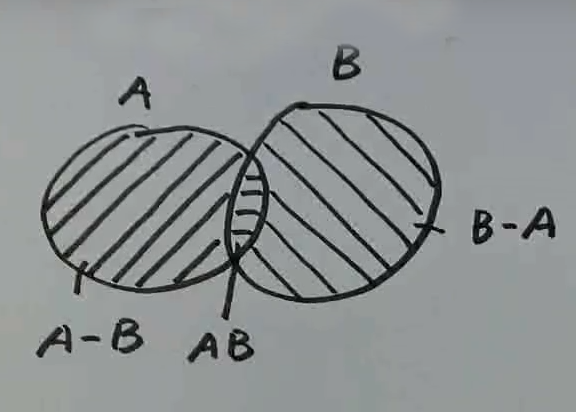
  • 差

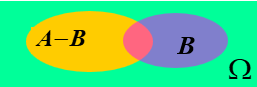
    • A发生且B不发生的事件称为A与B的差事件记作A-B

  • 补

    • A不发生的事件，称为A的补事件，记作$\overline{\text{A}}$

关系

设A，B两个事件

  • 包含

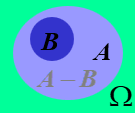
    • 若A发生，则B一定发生，成A包含于B，记作A$\subset$B

  • 相等

    • 若A发生，则B一定发生；反之，若B发生，则A一定发生，即A$\subset$B且B$\subset$A，称A，B相等，记作A=B

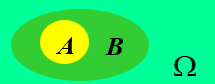
  • 互斥（不相容） A，B不能同时发生，称A，B互斥
    A，B互斥⇔AB=∅

  • 对立

    • A，B不能同时发生，且至少一个发生，称A，B对立

Notes:

  • A = ( A - B ) + AB
  • A + B = ( A - B ) + AB + ( B - A)

概率、概率的基本公式

概率的定义

E为随机试验，Ω为样本空间，∀A⊂Ω，定义P(A)，若满足：

  • ∀A⊂Ω，有P(A)≥0(非负性)
  • P(Ω)=1(归一性)
  • 设A1,A2,…,An,…,两两互斥，有P(A1+A2+…)=P(A1)+P(A2)+…(可列可加性)

称P(A)为事件A的概率

注：

  • P(∅)=0

    • 证明：取A1=A2=…=∅，A1,A2两两互斥
      P(∅+∅+…)=P(∅)+P(∅)+…
      ⇒P(∅)=P(∅)+P(∅)+…
      ∵P(∅)≥0
      ∴P(∅)=0

  • 有限可加性 ，设A1,A2,…,An两两互斥，则有P(A1+A2+…An)=P(A1)+P(A2)+…+P(An)

    • 证 ：
      令An+1=An+2==…=∅
      A1,A2,…,An,…,两两互斥
      则P(A1+A2+…An+…)=P(A1)+P(A2)+…P(An)+…
      ⇒P(A1+A2+…An)=(A1)+P(A2)+…P(An)

  • (补性质)A+$\overline{\text{A}}$=Ω，且A$\overline{\text{A}}$=∅ ，则P($\overline{\text{A}}$)=1-P(A)

    • 证
      ∵A$\overline{\text{A}}$=∅
      ∴P(A+$\overline{\text{A}}$)=P(A)+P($\overline{\text{A}}$)
      又∵A+$\overline{\text{A}}$=Ω
      ∴P(A+$\overline{\text{A}}$)=P(Ω)=1
      ⇒P(A)+P($\overline{\text{A}}$)=1
      ⇒P($\overline{\text{A}}$)=1-P(A)

概率的基本公式

减法公式

A=(A-B)+AB
且A-B与AB互斥
∴P(A)=P(A-B)+P(AB)
∴P(A-B)=P(A)-P(AB)
又A=AΩ=A(B+$\overline{\text{B}}$)=AB+A$\overline{\text{B}}$
∵AB⊂B,A$\overline{\text{B}}$⊂$\overline{\text{B}}$
∴AB与A$\overline{\text{B}}$互斥
∴P(A)=P(AB)+P(A$\overline{\text{B}}$)
⇒P(A$\overline{\text{B}}$)=P(A)-P(AB)
∴P(A-B)=P(A$\overline{\text{B}}$)=P(A)-P(AB)

加法公式

A+B=(A-B)+AB+(B-A)
且A-B,AB,B-A两两互斥
∴P(A+B)=P(A-B)+P(AB)+P(B-A)
∵P(A-B)=P(A)-P(AB),P(B-A)=P(B)-P(AB)
∴

  • P(A+B)=P(A)+P(B)-P(AB)
  • P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)